How To Use The Nernst Equation

Resting Membrane Potential -
Nernst Equilibrium Potential

In the previous section of this lecture (Establishment of the Membrane Potential), we learned the two requirements for establishing a membrane potential: (ane) ion concentration gradient across the membrane, and (2) selective ion channels in the membrane. We learned that the concentration gradient (i.east., chemical gradient) causes the ion to move from the compartment with the higher ion concentration to the compartment with the lower ion concentration. We learned that the movement of an ion across the membrane that is not balanced by the movement of a counter ion leads to charge separation beyond the membrane, and that this accuse separation forms the footing for the establishment of a potential difference across the plasma membrane (i.e., membrane potential, Five _k). Charge separation across the membrane leads to the establishment of an electrical gradient that grows in magnitude until it exactly balances the chemical gradient. When the chemical and electrical gradients are equal in magnitude, the ion is said to be in electrochemical equilibrium, and the membrane potential that is established at equilibrium is said to be the equilibrium potential (5 _eq.) for that ion under the existing concentration gradient.

Now allow�due south examine the chemic and electrical gradients more closely so that nosotros tin can gain a quantitative understanding of these two forces that human action on ions. Our ultimate goal is to go far at an equation that volition permit united states to calculate the value of the equilibrium potential based on the nature of ion (i.eastward., valence of the ion), as well as the ion concentration gradient that exists beyond the membrane. Hither, we take a simplified arroyo to deriving this equation. A more than rigorous arroyo is discussed under Derivation of the Nernst Equation. We will use Thousand⁺ for this derivation and will afterward extend the equation to other ions. We begin by determining the gratuitous energy (ΔG) bachelor from the chemical and electrical gradients. The chemical slope (ΔG_Chemic) and the electric gradient (ΔG_Electrical) can be divers as:

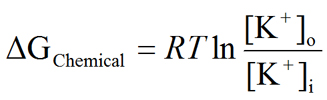Eq. 1

and

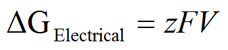Eq. ii

where R is the gas abiding, T is the absolute temperature, F is the Faraday abiding, 5 is the voltage, and z is the valence of 1000⁺ (+1). At equilibrium, ΔG_Electrical and ΔK_Chemical are equal. Therefore,

Eq. 3

Substituting for Δ1000_Chemical and ΔG_Electrical, we get

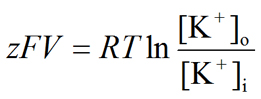Eq. iv

Solving for V, we become

Eq. 5

The in a higher place equation (Eq. five) is known as the Nernst equation. The Nernst equation allows us to calculate the potential that will be established across the membrane based on the valence and concentration gradient of K⁺ (provided that only K⁺ channels are nowadays). This potential is also referred to as the Nernst potential. The Nernst potential for any given ionic species is the membrane potential at which the ionic species is in equilibrium; i.e., at that place is no net motion of the ion beyond the membrane. Therefore, the Nernst potential for an ion is referred to every bit the equilibrium potential (5 _eq.) for that ion. At the equilibrium potential, the chemical and electrical gradients are equal and reverse in direction. For case, the Nernst potential for One thousand⁺ is the equilibrium potential for K⁺ (Five _{One thousand}). The generalized class of the Nernst equation is:

Eq. 6

where,

• V _eq. is the equilibrium potential (Nernst potential) for a given ion. It is common to use the ion symbol equally a subscript to denote the equilibrium potential for that ion (e.g., 5 _Thou, V _Na, V _Cl, V _Ca, etc.). If but ane ionic species is present in the organization and channels for but the ionic species are present (and open), then V _eq. will also exist the membrane potential (V _g). Note that the unit of Five _eq. is the Volt. However, the equilibrium potential is typically reported in millivolts (mV).
• R is the universal gas constant and is equal to 8.314 J.K⁻¹.mol⁻¹ (Joules per Kelvin per mole).
• T is the temperature in Kelvin (Thou = °C + 273.xv).
• z is the valence of the ionic species. For example, z is +1 for Na⁺, +one for G⁺, +2 for Ca²⁺, −1 for Cl⁻, etc. Note that z is unitless.
• F is the Faraday's constant and is equal to 96,485 C.mol⁻¹ (Coulombs per mole).
• [Ten]_out is the concentration of the ionic species X in the extracellular fluid. Notation that the concentration unit must match that of [X]_in.
• [X]_in is the concentration of the ionic species X in the intracellular fluid. Note that the concentration unit must match that of [X]_out. Typically, but non ever, the concentrations are noted in mM.
• The Nernst equation tin be derived based on simple thermodynamic principles (run across Derivation of the Nernst Equation).
• The Nernst potential calculator may exist used not only to perform calculations, simply likewise to gain a good agreement of this equation.
• If two or more ions contribute to the membrane potential, the Nernst potential no longer yields the V _m. In this instance, use the Goldman-Hodgkin-Katz (GHK) equation to calculate the V _m.

Nosotros should examine the Nernst equation closely in order to gain an intuitive understanding for the Nernst potential. First, it is reiterated hither that for the Nernst potential to exist established, selective channels must be present and open. 2d, by examining the Nernst equation, it becomes immediately obvious that just three factors are important in determining the magnitude and direction of the Nernst potential. These iii factors are (i) the concentration gradients, (2) the valence of the ionic species in question, and (3) temperature. If at that place is no concentration gradient across the plasma membrane, the ratio of the extracellular to intracellular concentration terms becomes i. The natural logarithm of 1 is zero. Hence, there volition be no potential deviation across this membrane, even if the channels for the ion were fully open up. Therefore, a concentration difference is essential in establishing a Nernst potential. The valence of the ion besides influences the magnitude and management of the Nernst potential for the ion. Note that the Nernst potential varies indirectly with the ionic valence. Temperature (T) also plays a small part in determining the magnitude of the Nernst potential. A few examples are presented below to show how the Nernst equation is used to make up one's mind the equilibrium potential for diverse ions.

If the ion in question is K⁺, the Nernst equilibrium potential for K⁺ (5 _Thou) will be:

Eq. 7

If the ion in question is Na⁺, the Nernst equilibrium potential for Na⁺ (V _Na) volition be:

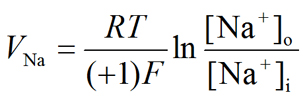Eq. 8

If the ion in question is Ca⁺, the Nernst equilibrium potential for Ca^two+ (V _Ca) will be:

Eq. 9

If the ion in question is H⁺ (hydrogen ion or proton), the Nernst equilibrium potential for H⁺ (Five _H) will be:

Eq. 10

If the ion in question is Cl⁻, the Nernst equilibrium potential for Cl⁻ (V _Cl) will exist:

Eq. 11

If the ion in question is HCO_iii ⁻ (bicarbonate), the Nernst equilibrium potential for HCO₃ ⁻ (5 _HCO3−) will exist:

Eq. 12

If the ion in question is SO_four ²⁻, the Nernst equilibrium potential for And so₄ ²⁻ (V _SO4−−) volition exist:

Eq. xiii

and so on.

For a typical mammalian jail cell in its natural environment (37 °C), the following ionic equilibrium potentials can exist calculated. The Nernst Potential Estimator tin exist used to perform these calculations.

Tabular array one. Intracellular and extracellular concentrations and Nernst equilibrium potential values for a few ions of physiological importance

Ionic Species	Intracellular Concentration	Extracellular Concentration	Equilibrium Potential
Sodium (Na+)	15 mM	145 mM	Five Na = +60.sixty mV
Potassium (K+)	150 mM	iv mM	V Chiliad = −96.81 mV
Calcium (Ca2+)	lxx nM	2 mM	5 Ca = +137.04 mV
Hydrogen ion (proton, H+)	63 nM (pH 7.2)	xl nM (pH 7.4)	V H = −12.13 mV
Magnesium (Mgtwo+)	0.v mM	1 mM	V Mg = +9.26 mV
Chloride (Cl−)	10 mM	110 mM	V Cl = −64.05 mV
Bicarbonate (HCO3 −)	15 mM	24 mM	5 HCO3- = −12.55 mV

If there are only One thousand⁺ channels in a cell, then V ₁₀₀₀ in this cell will be the same as the K⁺ equilibrium potential (V ₁₀₀₀) which tin be obtained from the Nernst potential for K⁺. Therefore, in this jail cell, V _chiliad = V _rest = V _K, which is what you lot expect because K⁺ distributes itself across the membrane co-ordinate to the Nernst equation which describes the situation at equilibrium (of form, the K⁺ channels have to be open to allow K⁺ to redistribute itself beyond the membrane according to the chemical and electrical potential gradients). At V _Thousand, at that place is no net movement of K⁺ across the membrane. Similarly, if there are only Na⁺ channels in the cell (and are open), at equilibrium, V _m = V _rest = V _Na. If there are only Cl⁻ channels in the cell (and are open), at equilibrium, V _yard = 5 _residuum = V _Cl.

If there are more than than one type of channels that are open up at whatsoever given time, the situation is slightly more than complex (see next section for details). At present the resting potential can no longer exist described as an equilibrium potential because no ion is at equilibrium (V _m = Five _rest ≠ V _eq.). This is because many ions are contributing to the resting potential, and the final value of the resting potential will depend on the concentration gradients and the relative membrane permeabilities of the ions in the system. When multiple ions are present, each ion is moving down its own electrochemical potential gradient. In this example, the organisation is said to exist at steady-state. Although there are exceptions, in nearly mammalian cells, the major ions contributing to V _rest are 1000⁺, Na⁺, and Cl⁻. In the next department, we will describe how different ions contribute to the membrane potential in real cells.

Posted: Saturday, February xv, 2014

How To Use The Nernst Equation,

Source: https://www.physiologyweb.com/lecture_notes/resting_membrane_potential/resting_membrane_potential_nernst_equilibrium_potential.html

Posted by: mcnealaune1955.blogspot.com

Share this post